Dividing Fractions | ||
| ||
Introduction | ||
This lesson will inform you how to divide fractions. Here are the sections within this lesson page:
|
Before progressing with this lesson, it is strongly recommended that you have a firm grasp of fraction multiplication. Dividing fractions relies on it. So, please review our lesson on fraction multiplication before moving on with the sections below.
| |
Say you found $20 and you wanted to equally share your finding with three friends. If the four of you were to take an equal portion of the $20, each of you would receive $20/4 or $5. Twenty divided by four… It is an easy problem. However, if you asked yourself ‘How many 50-cent pieces are there in $20?” it would lead to a harder problem, mathematically speaking. The problem demands that we divide the 20 by a 1/2 dollar.
In the section Example 1, we will see how to mathematically perform this task.
| |
To divide fractions, carry out these two steps.
| |
Here is our first example:
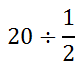
Following our steps, first we must first take the reciprocal of the second fraction.
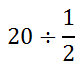
We can see that 2 divided by 1 is 2. So, our problem is now…
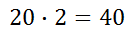
This answers our question from our previous section. There are 40 half-dollars in $20.
| |
Here is our second exmaple.
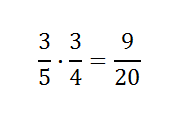
The Steps tell us to: 1) take the reciprocal of the second fraction and 2) switch to multiplication.
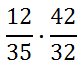
Now, we will reduce. Starting with the 12 and 32, we get this.
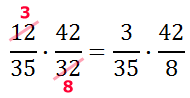
Now, we can reduce the 42 and the 35.
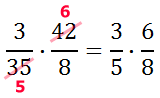
We can still reduce some more. Look at the 6 and 8. They can both be divided by 2 because they are even numbers.
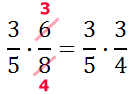
Since no remaining numerator has any factor in common with any remaining denominator, we need to multiply across to obtain the solution.
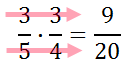
| |
So far, we have seen examples that describe how to perform tasks that lead to correct answers. However, it is worth mentioning the mathematics behind this process. Why? Mathematics is more than about mindlessly following tasks. Knowing why it works is important for deep understanding of this topic and all of mathematics. Here is a problem.
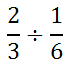
This horizontal layout can be changed to a vertical layout, like so because a fraction is really a division problem.
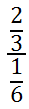
To simplify the fraction in the denominator of our compound fraction (the 1/6), we can multiply it by its reciprocal, which is 6/1. However, if we multiply the bottom of a fraction by 6/1, then we must also multiply the numerator by the same quantity. Doing so maintains the value of our complex fraction. So, let us now multiply both the numerator and the denominator of our compound fraction by 6/1.
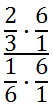
Cleaning up the denominator, we get…
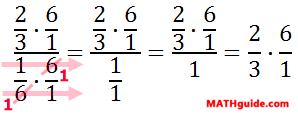
It is clear now that when we place our original problem next to this result, we can see that our Two-Step Process is accurate.
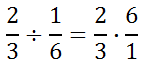
We can see that a division problem can be altered to a multiplication problem if we flip the second fraction.
Since we only wanted to understand the underlying process behind the steps, we will stop here. [The final answer is 4.]
| |
Use this instructional video to learn how to divide fractions.
| |
Use this interactive quiz to determine if you can divide fractions.
| |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: