Complex Counting | ||
| ||
Introduction | ||
In this section, you will learn how to use the formulas for combinations and permutations for various problems. Here are the sections within this lesson:
|
When counting complex problems, we will use something called a 'factorial.' A factorial looks like an exclamation point; like this:
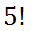
It means this:
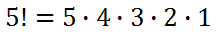
In general, it means this:
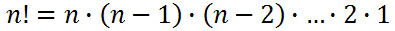
In the next section, we will learn about two problems that can use factorials as a means for solving them.
| |
Let's look at two problems that involve factorials. Problem 1:
If there are 8 different books on a shelf, how many ways are there to arrange those books? Imagine placing all the books on the floor. One would have to choose between 8 different books to be placed first on the shelf. Once picked, there would be 7 books remaining that could also be picked for the second place on the shelf. Once that book is placed on a shelf, there would be 6 books to choose from, and so on. Using the fundamental counting principal, the math would look like this.
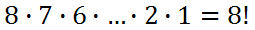
There are 40,320 ways to arrange these 8 books.
Problem 2:
If there are 4 people who need to be seated at a circular table, how many different ways can this be done? It appears this problem is the same as problem #1 above but it has less objects to arrange. We could list all the possibilities. We will list the people as person A, person B, person C, and person D.
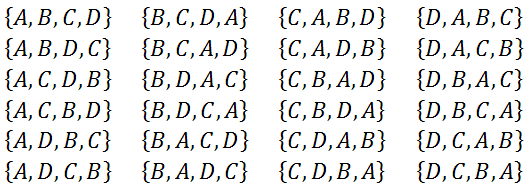
The problem with this list, which lists all combinations of A, B, C, and D, it does not take in to consideration that there is a circular table. However, it is a great list for placing people in a line. The difference is, there are situations listed there that are the same. Here are arrangements that are exactly the same, because of the circular situation.
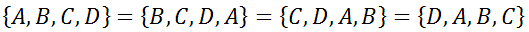
Take any letter. Look to its left and right and you will see identical adjacent letters in each set. This means the only true unique situations we can gain is by looking down one of the columns from our large 24-set list above. So, there really are only 6 unique arrangements. This means if we take one less than our number of people, we can simply use factorials.
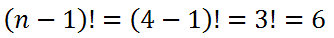
There are 6 ways to arrange 4 people at a circular table. Note: This means if we started with 8 people, we could calculate the total possible ways to arrange them around a table by calculating 7!, which is 5,040.
| |
If one were to award prizes to runners in a race, it is interesting to calculate how many ways prizes can be awarded. Imagine having two $20 prizes to give to the first two winners of the race. If there were 5 runners in the race, we can see how many ways we can get two winners. We can list the runners as numbers, as if we gave them tags to wear.
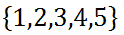
Here are all the possible winning pairs:
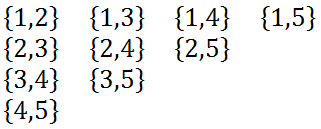
Note that we cannot list {3,1} as a possible pair in addition to {1,3} because doing so would count the same pair of runners twice. Therefore, there are 10 possible outcomes.
We will see in the next section that there is an easier way to calculate these situations because listing all subsets if there were 200 runners would be very impractical.
| |
When there are 'm' runners and we are to give out 'n' awards, there is a formula to use.
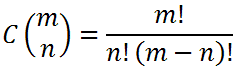
Sometimes, this formula is referred using several methods, such as these:
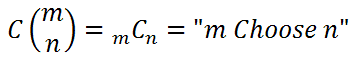
Note: This formula is used when there is no significance to order of outcomes.
| |
Now, we will use the combination formula from the last section for two problems. Problem 1:
If 300 tickets were sold for a raffle, how many ways could 5 $20 awards be given? There are 300 tickets and we will choose 5 winners, like so.

The work above demonstrates how one can simplify the problem using the combination formula. Most people do not do the work above and instead use the built in combination functionality of a calculator to get the final answer. The answer is roughly 19,582,837,560 combinations or over 19 billion different ways winners can be awarded.
Problem 2:
If 5 cards are dealt from a standard deck of cards, how many ways are there to do this if order is not important? We simply need to use the formula for a standard 52-card deck. We will use "52 choose 5."
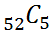
Simply plug this into a scientific calculator (or a better calculator) to get 2,598,960, which is over 2.5 million possible outcomes.
| |
Permutations describe counting subsets when order matters. When referring to racing horses and coded locks, we know that order does matters. When we calculate permutations, like how many ways can 8 horses place first, second, and third place, we would use this formula.
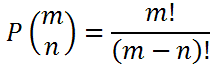
The problems in the next section will reveal how to use this formula.
| |
The problems in this section will indicate how to use the permutation formula, which was described in the previous section. Problem 1:
How many ways can 8 horses place first, second, and third place? For our horse race situation, we would take 8 horses and place 3, like this.
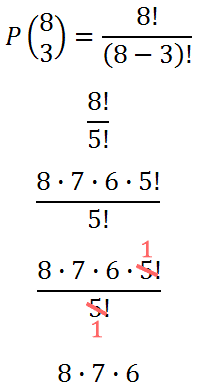
There are 336 ways to have 8 horses place for 1st, 2nd, and 3rd place. The work above demonstrates how one can simplify the problem using the permutation formula. Most people do not do the work above and instead use the built in permutation functionality of a calculator to get the final answer.
Problem 2:
At a certain school, there are 850 seniors. From this group, a president and vice-president will be chosen. How many ways can this be done?This is another problem that involves order. When we choose two people from the large group, the first person will be the president and the second person will be the vice-president. So, we will take 850 and order 2, like so.

This means there are 721,650 possible ways to pick these two positions. The work above demonstrates how one can simplify the problem using the permutation formula. Most people do not do the work above and instead use the built in permutation functionality of a calculator to get the final answer.
| |
Try our instructional videos to determine if you understand the lessons above.
| |
Try our interactive quizzes to determine if you understand the lessons above.
| |
Examine our activities related to the lessons above.
| |
Try these lessons, which are closely related to the lesson above.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: