Power Rules of Exponents | ||
| ||
Introduction | ||
In this section, you will learn a variety of properties and applications involving logarithms. Here are the sections within this lesson:
|
An exponent is written as a little number to the top right of either a number or variable. Take for instance 2-cubed, which is written as:
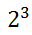
The little 3 means we multiply three factors of two, like so.
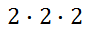
If we multiply these twos, we get the value 8. So, 2-cubed is equal to 8. If we are going to get technical, the 2 is called the base and the 3 is called the exponent (or power). Sometimes we will refer to the base when we speak in general terms that are unrelated to a specific problem. In general, we could write this expression.
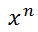
With the 'x' as a base and 'n' as an exponent, this expression really means...
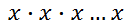
...or 'n' factors of 'x.'
The next sections will explain several power rules.
| |
Consider simplifying this expression.
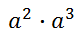
If we write what a-squared and a-cubed mean, we can come to an understanding about how to simplify this expression. So, we need to first make two factors of 'a' and then three factors of 'a,' like so.
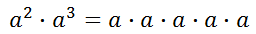
We can clearly see that there are now five factors of 'a.' This means our expression can be simplified to...
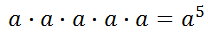
To generalize this process, we can write this.

| |
Consider this expression.
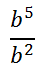
Again, let us expand the expressions in the numerator and denominator to get a better idea how to simplify the fraction.
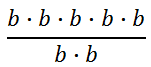
Now, reduce the fraction by "canceling" like factors.
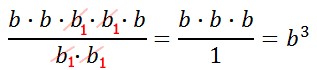
We can get that same solution much faster if we subtract exponents.
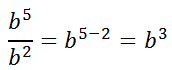
In general, this means...

Notice how this rule is closely related to the Power Rule of Multiplication. When multiplying like bases, we add exponents. If we divide like bases, logic would tell us we should respond with subtraction because subtraction and addition are inversely related.
| |
Consider this expression.
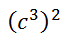
If we think of the outside exponent of two to mean making two factors, we get this expression.
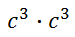
Using the Multiplying Like Bases rule, we get this.
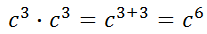
However, if we place the problem and solution next to each other, we should be able to see a quicker way to arrive at the solution.
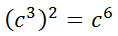
Clearly, we can see that 2 times 3 is equal to 6, which leads us to the general rule.

| |
Let us examine a variation of our Dividing Like Bases situation.
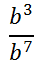
Using the rule, we get...
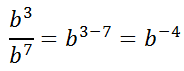
We get a negative exponent. To determine what a negative exponent means, we have to expand the numerator and denominator by going back to the basics.
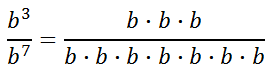
Reducing this, we get...
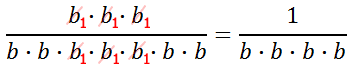
We can condense the denominator, like so.
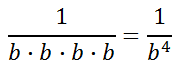
Let us look at the negative exponent and the final solution.
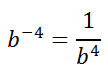
We can conclude that negative exponents simply mean there are factors that remain, but they are in the denominator. It also helps us arrive at a generalization.
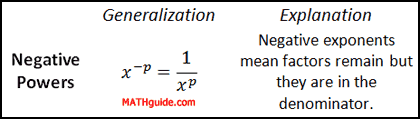
| |
Again, let us look at another variation of our Dividing Like Bases situation. Let us see what happens when the numerator and denominator have an equal number of common factors. Look at this problem.
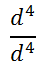
Let's use the rule.
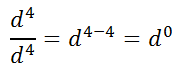
But, what does this zero exponent really mean? One way we can find out the answer to that question is to expand the numerator and denominator.
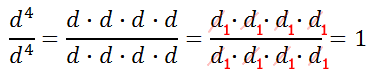
Keep in mind that that the d-value cannot be equal to 0 because we cannot divide by zero. For all other non-zero values of 'd'...
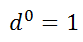

| |
Look at this expression with 'f.'
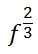
It really means this radical expression.
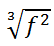
Notice that the denominator of the fractional power refers to the type of radical. In this case the radical is a cube-root because the denominator of the fractional power was a three. Three means cube but in this situation it is cube-root. Examine this radical expression.
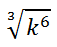
It really means this fractional power expression.
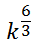
Consequently, we can simplify this expression.
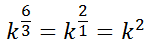
Sometimes it is easier dealing with fractional powers than it is radical expressions and vice-versa. Yet, here is the generalization.

If you would like to know why this relation is true, read the section called Rationale of Fractional Powers.
| |
Here is a graphic organizer that contains all the power rules for exponents.

| |
In the section above, called Fractional Powers, we saw how fractional powers are related to radical expressions. This section will explain why that relation is true. Consider this expression to understand exactly what fractional exponents represent.
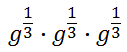
We know from the Power Rule of Multiplication that we have to add the exponents.
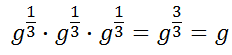
The only way this makes sense is if we are multiplying radical expressions, like so.
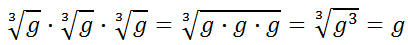
Likewise, consider this.
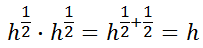
This, too, must mean we are referring to radical expression.
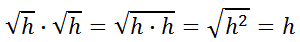
In short, this indicates fractional powers really mean radical expressions.
| |
Try our interactive quizzes to determine if you understand the lessons above. This quiz creates six different random problems in random order.
See if you can use the Power to a Power Rule to change the base in a formula that contains a complex exponent.
| |
These lessons are related to the lesson above.
| |
 uiz:
uiz:  esson:
esson: