Solving Complicated Proportions | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn about proportions. Here are the topics within this page:
|
Proportions are used for a variety of goals: determining a 'normal' weight for a baby at a certain age, calculating distances on maps, identifying inventory rates for businesses, ... MATHguide has a lessons that explains the mathematical nature of proportions, if you require a refresher on the topic.
The sections that follow will allow you to understand how to solve complicated proportions that lead to linear and quadratic equations.
| |
The second type of complicated proportion leads to linear equations. Before progressing, you will need to know how to solve linear equations. Review this lesson, if necessary, before progressing.
Take a look at this example to see how to solve a complicated proportions. Example: Solve this proportion.
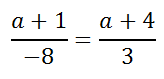
We know from our knowledge of proportions (see Proportions) that cross-products must be equal. So, cross-multiply.
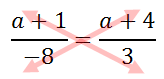
Cross-multiplying results with these two equal products.
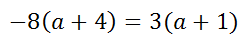
The steps that follow will indicate how the linear equation can be solved for the a-value. Do the distributive property.
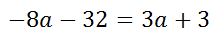
Subtract 3a from both sides of the equation.
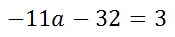
Add 32 to both sides of the equation.
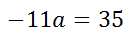
Divide both sides of the equation by -11.
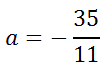
Rounded to the nearest 10th, the solution is...
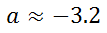
This video will inform you as to how to solve this type of complicated proportion.
Try these interactive quizmasters to determine if you have the hang of it.
| |
The first type of complicated proportion leads to quadratic equations. Before progressing, you will need to know how to solve quadratic equations. Review this lesson, if necessary, before progressing.
Review this example, which will demonstrate how to solve complicated proportions. Example: Solve this proportion.
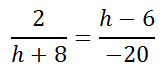
Like the problem in the previous section (see Solving Complicated Proportions), we can use the cross-products to begin on our journey to solve for the h-value.
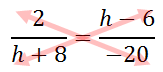
Here are those cross-products.
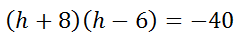
Multiply the two binomials. A multiplication table is best here (see Multiplying Polynomials for help).
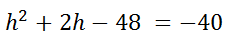
Add 40 to both sides of the equation.
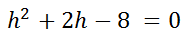
Now, factor the trinomial (see Factoring Trinomials for help).
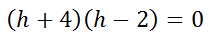
Next, we set the factors equal to zero (see for help).
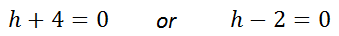
Last, we solve each equation separately to gain two solutions.
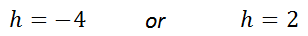
Note, be careful to look at the denominators of our original problem. We have to be careful not to get a zero in a denominator because zero denominators are illogical and therefore unacceptable. If we substitute h=-4 into the original problem, the denominator is not equal to zero, making it a possible solution. For the same reason, h=2 is another acceptable solution. This video will inform you as to how to solve this type of complicated proportion.
Try this interactive quizmaster to determine if you digested the lesson above.
| |
Here are instructional videos that explain all the aspects of solving complicated proportions.
| |
Try these quizmasters to determine if you understand how to solve complicated proportions.
| |
These lessons are related to solving complicated proportions.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: