Properties of Quadrilaterals | ||
| ||
Introduction | ||
This lesson page will inform you about the properties of quadrilaterals. Here are the sections within this lesson page:
|
A quadrilateral is a polygon that has four sides. Quadrilaterals are sometimes called tetragons (4-sided polygon, like hexagons have 6-sides) or quadrangles (having 4-angles, like triangles have 3-angles). | |
Besides having four sides and four angles, there is a property concerning its angles. Look at this quadrilateral ABCD.
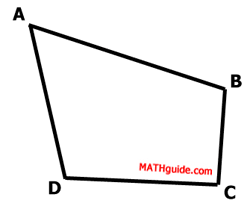
If we draw diagonal (a segment that connects two non-adjacent vertices) BD, we can see the quadrilateral is divided into two triangles.
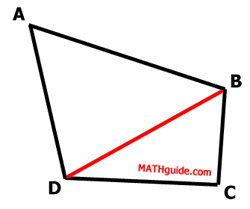
One property of a triangle (in a plane) is that the sum of its internal angles is 180 degrees. Each triangle therefore has a sum of 180 degrees.
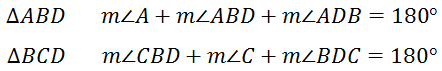
If we add all of these angles, we get...
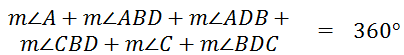
Let's rearrange these angles, like so...
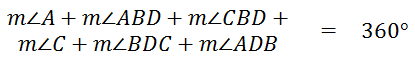
We can see from the diagram that angle-ABC and angle-ADC have been broken into two smaller angles.
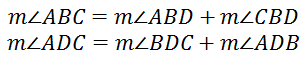
So, we can make a substitution within our rearranged 360 degree equation. We can take pairs of angles and replace them.
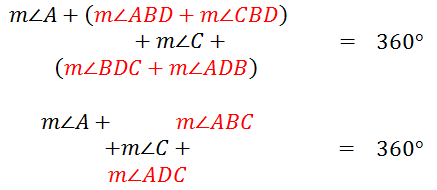
Removing the diagonal, we see our original quadrilateral.

We therefore no longer need to use three letters to describe our angles. This makes the equation a lot simpler.
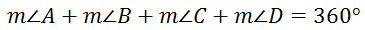
This means...
Interior Angles is Always Equal to 360 Degrees | |
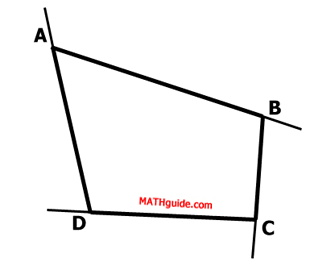
Below is quadrilateral ABCD again.

Here is the same quadrilateral with exterior angles shown.
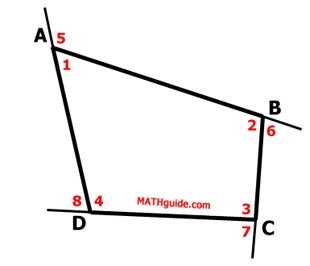
The angles need to be marked so that another property can be found.
Notice the supplementary angles.
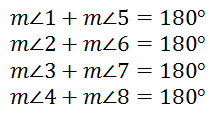
If we add all of these equations, we get this new equation.
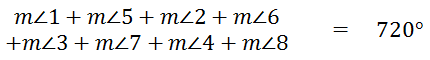
We can rearrange the angles, like so.
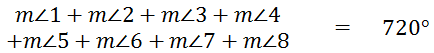
From the last section (Interior Angles) we discovered that the sum of the internal angles is always 360 degrees. So the sum of angles 1, 2, 3, and 4 has to be 360 degrees. The equation now becomes...
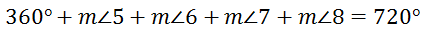
We can subtract 360 degrees from both sides of the equation to get this equation.
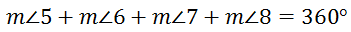
This means...
Exterior Angles is Always Equal to 360 Degrees | |
Review this related lesson.
| |
 esson:
esson: