Chord-Chord Relationships | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn a variety of relationships within a circle that involve chords and arcs. Here are the topics within this page:
|
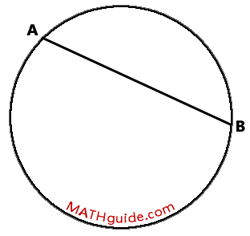
Within this page, we are going to examine segments within a circle. Segments that have their endpoints on a circle are called chords. The figure below shows chord AB.
The longest chord of a circle has a special name. It is called a diameter, which is shown below as chord CD.
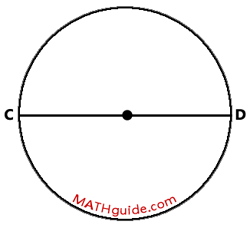
Notice how chord CD passes through the center of the circle. Learn more about other terminology related to circles in this MATHguide lesson.
The sections that follow will address various properties that involve either partial lengths of chords or arcs and angles.
| |
Within this section, we will explore the relationships of lengths between intersecting chords of a single circle. Examine this diagram to view intersecting chords RS and TU.
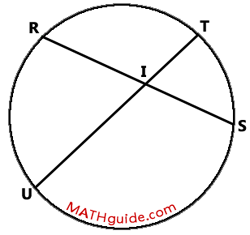
The two chords intersect at point I. Consequently, each chord is fractured into two pieces. Chord RS is split into segments IR and IS and chord TU is split into segments IU and IT. The mathematical relationship that exists can be written like this.
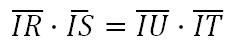
Sometimes it is more advantageous to write the relationship using words, like this.
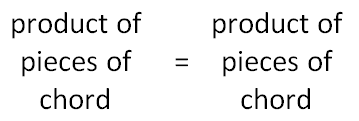
To see how this relationship is proven, watch this video.
Here is an example of how the relationship is applied. Example 1: Solve for the x-value shown in this diagram.
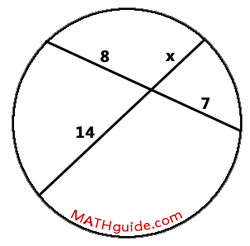
The diagram above has two intersecting chords. The relationship informs us that we must calculate the product of the pieces of one chord and set it equal to the product of the pieces of the other chord, like so.
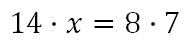
Finishing the relationship, we get this algebra.
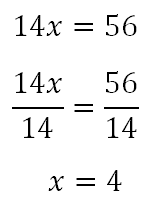
Example 2: Solve for the x-value shown in this diagram.
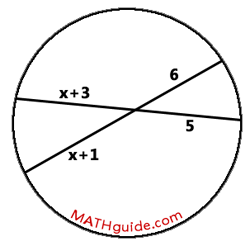
We will multiply the pieces of one chord and set the product equal to the product of the pieces of the other chord, like so.
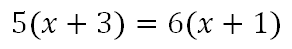
To solve, we will begin by using the distributive property. Then, simple algebra thereafter.
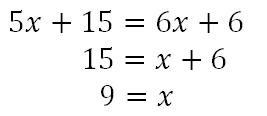
| |
When two chords intersect, there are certain arcs and angles that share an interesting relationship. Using the diagram below, we will share that relationship.
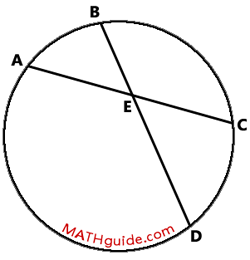
The relationship that ties together angles and arcs is this:
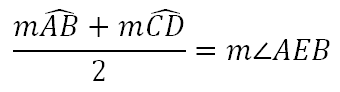
Notice how the intersecting chords also intersect the circle. Arcs AB and CD are both within angle AEB and its vertical angle CED. Another way to think of this relationship can be written like so.
We will now use this relationship to solve two problems. Example 1: Solve for the x-value shown within this diagram.
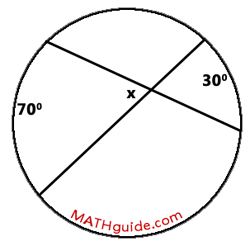
The arcs that are opposite the angle marked by the 'x' are 70 degrees and 30 degrees. According to the relationship, we will solve this equation for the x-value.
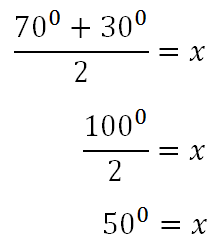
Example 2: Solve for the x-value shown within this diagram.
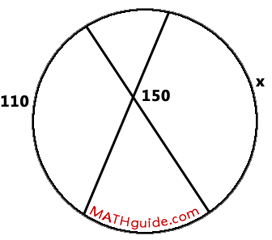
We will solve this problem by taking half the sum of the arcs and setting the result equal to the angle, like so.
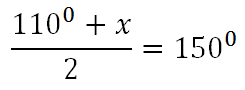
To solve this algebra problem, we will make the right side a fraction. Then, we will solve the resulting proportion by cross multiplying, like so.
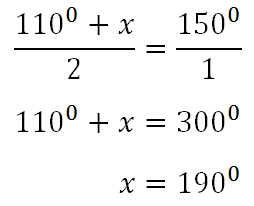
| |
View the following instructional videos.
| |
The following quizmaster will check for your understanding.
| |
There are no activities at this time. | |
Here are lessons that are related to chords.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: