Inscribed Angle and Arc Relationship | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn the relationship between inscribed angles and their respective arcs. Here are the topics within this page:
|
An inscribed angle is an angle that has its vertex on a circle and its sides are chords of the same circle. An inscribed angle can be seen here.
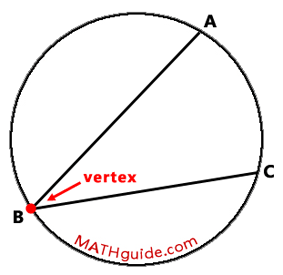
The diagram above shows inscribed angle ABC. The vertex of the angle, point-B, rests on the circle. The sides of the angle are chord AB and chord BC. The arc intercepted by the angle is arc AC.
Within the next section, we will examine the relationship between an inscribed angle and its arc.
| |
The relationship between an inscribed angle and its opposite arc can be seen below.

This relationship will be demonstrated by viewing the examples below.
| |
Determine the measure of angle HMS (the x-value) within the diagram that follows.
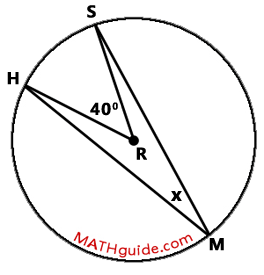
We know from our section on the Central Angle and Arc Relationship that a central angle and its intercepted arc are equal in measure. This means that arc HS is equal to 40 degrees.
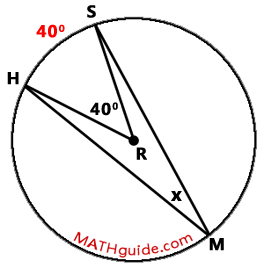
Notice that arc HS is the intercepted arc of inscribed angle HMS. We also know that the measure of an inscribed arcs is equal to half of its intercepted angle, which would make angle HMS. Therefore, angle HMS must be 1/2 of 40 degrees or 20 degrees.
| |
Determine the measure of angle CAB (the x-value) within the diagram that follows.
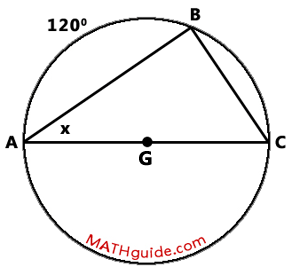
Notice how chord AC passes through the center of the circle, point G. This means that chord AC is a diameter of circle G. It also means that arc AC is a semi-circle and that its measure is 180 degrees. Arc AB and arc BC together have a sum of 180 degrees. This means that arc BC must be 60 degrees.
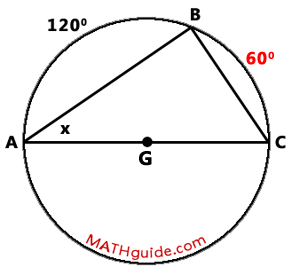
If we look closely at the diagram, we can see inscribed angle CAB and its intercepted arc, which is arc BC. Since inscribed angles are half the measure of their intercepted arc, angle CAB is equal to 1/2(60 degrees), which is 30 degrees.
| |
View this instructional video. | |
This quiz will check for your understanding. | |
There are no activities at this time. | |
Here are related lessons to the central angle and arc relationship.
| |
 ideo:
ideo:  ideo:
ideo:  esson:
esson: