Systems of Linear Equations | |||||||
| |||||||
Introduction | |||||||
In this section, you will learn how to solve systems of linear equations using many methods. Here are the sections within this page:
| |||||||
If we look at the coefficients on a single letter between the two equations and they are opposites of each other, then we can add the two equations to cancel that letter. We will gain an equation having a single variable that can be solved quite easily. After we obtain the value of one variable, we can then plug that value into an equation and solve for the other letter. Let's look at an example.
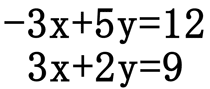 If we add the two equations, we will get ...
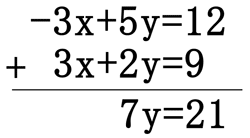 ... 0x + 7y = 21 or 7y = 21. If we divide both sides by 7, we get y = 3. Next, we substitute 3 in for y into any one of the equations. If we choose to substitute in the first equation, we get ...
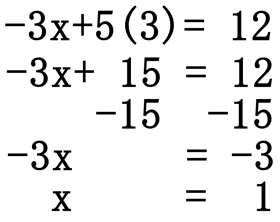 Since x = 1 and y = 3, the two lines intersect at (1, 3).
| |||||||
Most of the equations that we are presented with do not have coefficients that are opposite each other for a single variable like we saw for the example presented within the addition method above. It is more probable that our equations will need to be manipulated so we may use the addition method. The technique for preparing the equations is sometimes simple and other times more complicated. View the following example to get a feel for this this strategy.
Let us say we had to solve this system of equations.
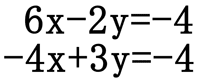 Adding the two equations as they are right now will not cancel any variable, nor leave us with a single variable. However, if the coefficients on the x-terms were opposite in value (like the problem from the addition method section above), we could add the system of equations to end up with a single equation with only one variable. This set of equations requires multiplying both equations by values so that the coefficients on either the x-values or the y-values are opposite in value. To achieve these opposite coefficients we could multiply the top equation by 4 and the bottom equation by 6 as such.
Or, we could multiply the top equation by 3 and the bottom equation by 2.
In either case, we can now use the addition method to cancel a single letter from each system, in order to be left with a single variable and one equation. We will leave the reader to verify that the solution is x = -2 and y = -3. It can be written as (-2, -3).
| |||||||
The substitution method is best used when a coefficient on a variable is equal to one. This is because will be simple to get a variable alone and proceed with this method. For instance, this system of equations has a variable that has a coefficient of one.
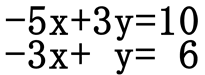 "Y" in the second equation has a coefficient of one. This will allow us to get the "y" variable alone without much effort. Simply add "3x" to both sides of the equation.
 Now that we have an equation solved for "y," we can now substitute it within the first equation. We will do this by replacing the "y" with "3x+6."
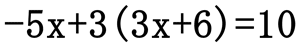 We have an equation with one variable, which will allow us to use basic algebra techniques to solve for "x," the remaining variable.
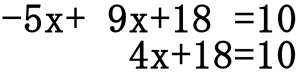 Subtract 18 from both sides, then divide both sides by 4 to get "x" alone.
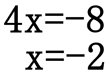 To solve for "y," substitute for "x" into the equation "y = 3x + 10" as such.
 Since x = -2 and y = 0, the two lines intersect at (-2, 0). If it becomes difficult to solve for a variable in a system of equations, the multiplication/addition method or linear combination method may be a better method to use. The substitution method is a valid method for all systems but the technique is cumbersome for many systems that have coefficients that are indivisible, called "relatively prime" to borrow terminology from number theory.
| |||||||
This video will demonstrate how to solve a system of linear equations using a method called Reduced Row Echelon Form (RREF) and a TI-Nspire calculator.
When dealing with systems of equations, it is possible to get three types of solutions: zero, one, or infinite solutions. This next video will demonstrate how to interpret augmented matrices for determining the number of solutions. | |||||||
This video will demonstrate how to solve a linear system of equations using a Matrix Equation. | |||||||
To solve a system of three equations and three unknowns, there is a strategy. The strategy is to reduce the "3 by 3" system to a "2 by 2" system. The way to do this has been thoroughly explained in this video.
| |||||||
Here are instructional videos to help you understand the lessons above.
| |||||||
Here are quizmasters related to the lessons above.
| |||||||
Use this game to learn about systems of equations.
| |||||||
Here are activities related to the lessons above.
| |||||||
MATHguide has these lessons and quizmasters that are related to the ones on this page:
|
 ideo:
ideo:  uizmaster:
uizmaster:  ctivity:
ctivity: 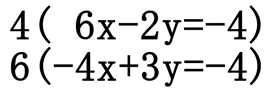
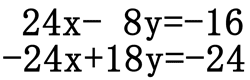
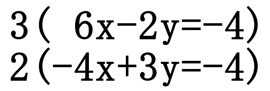
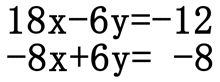
 ame:
ame:  esson:
esson: